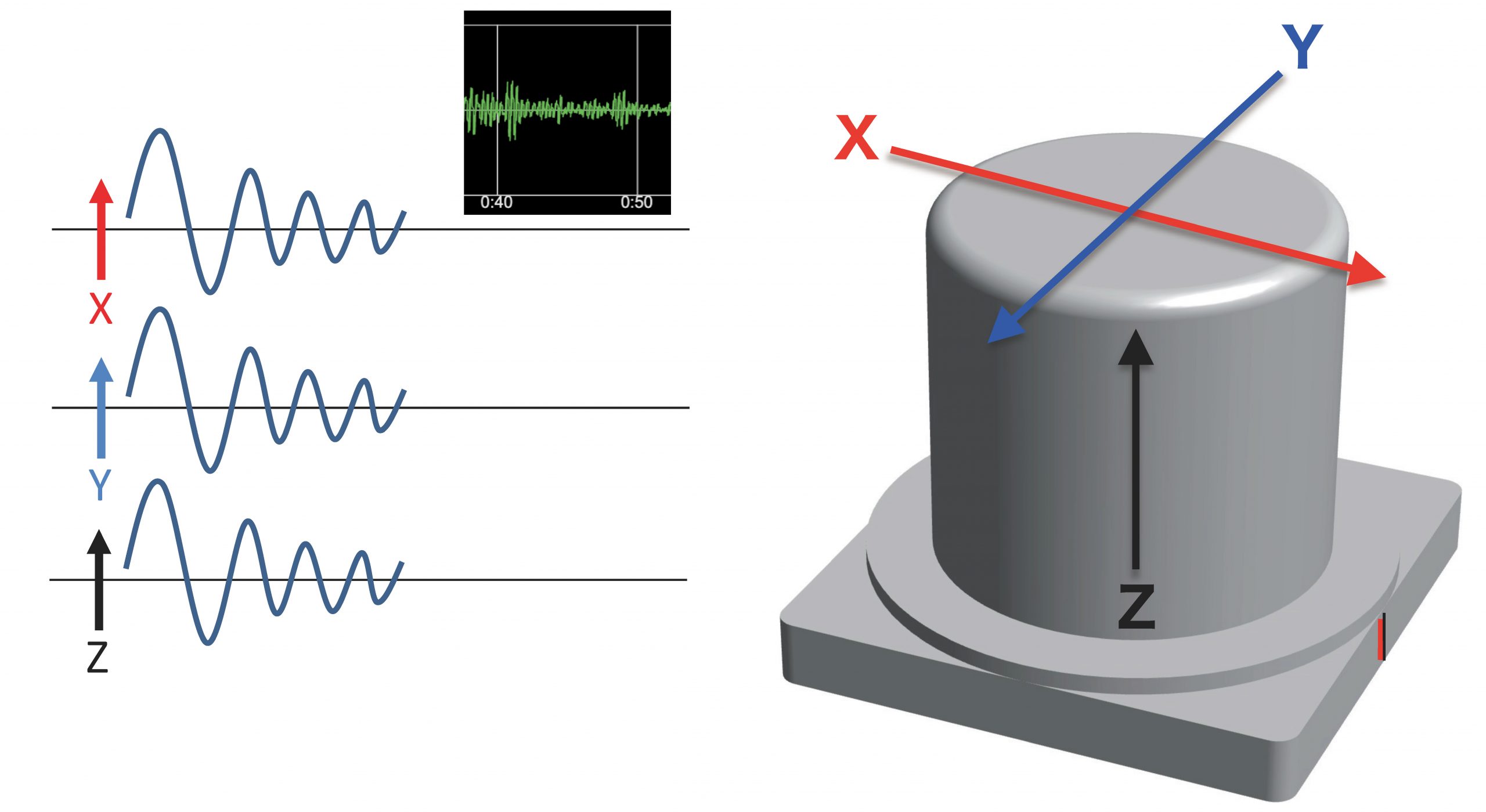
ブログ
地震計の物理学1-前口上-
| 本項 | 次へ 地震計の物理学2-道化師のダンス- |
この記事の目的と筆者の紹介
想定読者
この記事の想定読者は、地震に興味のある高校生、ちょうど微分方程式を学んでいる大学生、昔力学はちょっと勉強したけど突然計測震度計を扱わなきゃいけなくなった社会人、そして唐突に地震計について知らずにはいられなくなった稀有な大人である。中学生以下は対象としないが、微積分を一所懸命に学ぶ意欲があるなら大歓迎だ。そんなに難しい数学や物理学を扱わないように心がけるので安心して欲しい。そもそも難しい物理学や数学を扱えるほど筆者は賢くない。
この記事の目的
地震計の物理学と言っても、内容はほぼ1自由度の振動現象だ。そして地震観測には100年を超える歴史があるわけで、世の中には良い教科書がたくさんある。線形常微分方程式を解くと一般化してしまえばより厳密に扱っている数学の教科書が沢山あるし、1自由度系の振動現象と物理的に一般化すれば工学の教科書が沢山ある。もしちゃんと知りたいならそう言った教科書を読んでもらうほうがいいだろう。研究、教育において最前線を行く第一級の研究者が書いた教科書とブログ記事程度で張り合おうというのはあまりに傲慢な態度だろう。かと言って実際的な1自由度に上手く制限する機構や、振動を管理する電気回路等のノウハウにあたる話は流石に公にできないので、メーカーとして語れることは広く知れ渡っている内容に限られてしまう。公にできる話は今後紹介していけたらいいなと思う。
だから大切なのは想定読者だ。現在未来の専門家ではないお客さんや同僚が、地震計って結局なんなのさ?という疑問の答えをわかった気になれるくらいを目指すことにする。もしかしたらちゃんと勉強するためのとっかかりくらいにはなれるかも知れない。ゆっくり進めるので地震計の話だけでいいよという方は4章まで飛んでいただきたい。
文体に関してはファラデー先生の「ろうそくの科学」に従おうと思う。
さて、先に進める前に、もう一言言わせてください。われわれのテーマはとても壮大だし、それを真摯に、まじめに、科学的に取り上げようというわれわれの意図も壮大なものではあるんですが、でもわたし、われわれの中の年長者からは距離をおくつもりです。子供のみなさんには、自分も子供の一人として話すという特権をいただきましょう。これは前にもやったことだし、お気に召したらまた何度でもやります。そしてここに立って、自分がしゃべることばが世間一般に向けてのものだとわかってはいますが、それでもきみたちに話すときには、いちばん身近な人間に話すときみたいな、親しみをこめた話し方をするようにします。
-「ろうそくの科学(青空文庫)」著:マイケル・ファラデー 訳:山形浩生
もちろん私は年長者ではないし、読者が子供なわけでもない。テーマも意図もそこまで壮大でもない。ファラデー先生の意図を十分に汲み取れているかと言えば少し疑問もあるし、実現できているかと言えば大いに疑問がある。ただ、それを模倣しようとする意図を汲み取っていただければ幸いである。
さて、紹介するのは振動するって結局どう言うこと?と言う話。もしかしたら聞き覚えがあるかも知れないがいわゆる強制振動の話をしたい。難しく言うと、定数係数の2階線形微分方程式で振動する非斉次項を持つ非斉次方程式を解く。そして、そこからもう少し踏み込んで、地震計は振動現象の何を測っているのか。どう言う条件を整えてあげれば測れるのか。そして周波数特性ってなんなの?と言うところまでいきたい。厳密な議論はせず解も天下り式に与える。詳しいことは参考書を読んで欲しい。
その先のじゃあ実際のところその物理量をどうやって測るのか?どうやって電気信号に変換するのか?と言った話は別の機会にする。と言っても、大抵の検出器がやっていることはスピーカーと一緒で磁石の近くでコイルに電流が流れると動くと言う中学校で実験したかもしれないアレである。
ぶっちゃけよう。地震計の仕組みなんて知らなくても今時の地震計は扱える。業者に任せて適切に設置し、説明書通りに操作すれば何も知らなくても地震の波形を手に入れることができる。波形をわざわざ自分で解析しなくても計測震度を始め各種の演算を常時している。必要なら震度3を超えたらメールで知らせるなんて機能も勝島製作所の地震計なら標準装備だ。少数ロットの特注品は別にしても、そうでなければ量産される工業製品とは呼べないだろう。
もっと考えるべきは、計測した震度をどう危機管理に活かすべきかとか、波形データをどう解析し利用するかと言った測ったデータのこと。
それから、この地震計は雷に強いだとか、壊れにくいだとか、ずっと測っているから想定外に必要になった小さい地震の波形もちゃんと残っているとか、時刻精度が凄くいいからあちこちの波形データの位相を良く比較できるとか、常時1kHzでサンプリングしているとか、そう言った実際的な機械の話だ。もちろん並べたのは宣伝文句である。お声がけいただければご説明に伺いますので、是非購入をご検討ください。
長々と余計なことを書いたが、必要ないことをなぜ紹介し、学んで欲しいかと言えば、やっぱり基本的なことは大事だからだ。
例えば熱燗を用意する場合を考えよう。日本酒や焼酎が苦手ならホットワインでも構わないし未成年の方はホットミルクでもいい。もっとシンプルにお湯でもいい。というかお湯にしておこう。適当な容器に水を入れてお湯のたっぷり入った鍋の中に入れて温める。熱浴から得られる熱伝導で温まるのでお湯の量が十分多ければ容器が2つに増えても温める時間は変わらない。温度調整は結構頑張らなきゃいけない。現代では物を温めるのにもっと便利な道具がある。電子レンジだ。電子レンジはマイクロ波で出力をフルに使って水分子を温める。お手軽に温められるが、その仕組み上、量が二倍になったら時間も二倍になる。逆に言えば最適な時間を知っていれば突然「私の分も」と言われても焦らずに時間を二倍にすれば良いのだ。厳密には多少ずれるがまぁ誤差の範囲としよう。エネルギーについてちょっと知っていれば目標温度に対する加熱時間を簡単に計算してあげることもできる。600wは大体143cal/sだ。1calというのは1gの水を1°C加熱するのに必要なエネルギーだから、143gの水を600wで10秒加熱すればおよそ10°C温めることができる。ホットミルクやホットワインの適温は60°Cくらいらしいので、冷蔵庫から出してすぐの温度を5°Cくらい、コップ1杯およそ200gとして、200[g]×(60-5)[°C]/143[cal/s]≒77[秒]なので大体1分10秒温めればいいことがわかる。もちろん容器を温めるのにもエネルギーが使われるし、アルコール度数の低いお酒はともかくミルクを水と同等に扱っていいのかという問題はあるが、目安くらいにはなるだろう。何度か温めてみてグラフを書けば夏休みの自由研究くらいにはなりそうである。なお、温められるのは液体の水分子なので冷凍食品を解凍するのは簡単じゃない。冷凍食品メーカーも家電メーカーもこんな簡単な議論では済まないたくさんの工夫をしていて、とてもじゃないが一般消費者がそれら全てを追いかけることはできない。それでもその基本的な仕組みを知っていればより便利に使えるのだ。
地震計も同じである。知らなくても困らないが、ちゃんと知っておけばどこかで役に立つ。たぶん。少なくとも、他人行儀な「なんだかわからないが波形を出力する機械」ではなく、「ちゃんとこう言うものを測っている機械だ」と身近に感じられるようになるだろう。設置する目的によっては、よりよく地震計を選定できるかも知れない。もうちょっと言うと、うちの大事な可愛い地震計のことをよく知って好きになって欲しいのだ。もちろん、研究目的等でがっつり使いこなす必要のある人は機器の特性やら設置環境、施工方法、センサ毎の個体差までしっかり勉強したほうがいいだろう。ただここで色々全部書くわけにはいかない。余白はいくらでも用意できるが流石に手に余る。繰り返しになるが、しっかり理解する必要のある人はいい教科書を調達して勉強してほしい。この記事はなんとなく雰囲気を把握したり、勉強する足掛かりくらいの内容にとどめる。細かい話には企業秘密もある。そのあたりは商談の席でこっそりさせていただきたい。
筆者の紹介
本題に入る前に筆者の紹介をさせて欲しい。もちろんこの記事をより身近に感じながら読んで欲しいからだ。筆者は中学3年間をろくに勉強もせず過ごしたのち、稀有な機会に恵まれて高校時代3年間を伊賀の山奥で忍者の修行をして過ごした。ちなみに部活は演劇部だ。修行の甲斐あって大学に滑り込み理学部で物理を学ぶことが出来た。なんだちゃんと物理勉強しているじゃないかと思われるだろうが、その後約10年ほぼ触れることなく自分の精神と向き合う修行を積み、残念なことにそんな昔のことはほとんど忘れてしまった。幸いなのは生真面目な学生だったので高額な教科書を大学近くの古本屋に売るなどと言うことはせず全て手元に残っていたことだ。他にも会社の書庫にある沢山の地震の教科書にも助けてもらった。おかげでこの記事を書くことができる。色々書いたが実質的には昔物理をかじった30過ぎの新人営業課員Aが昔を思い出しながら四苦八苦しつつ書いていると思って欲しい。そして、ここまで読んでくださった奇特な方はもうご存知かと思うが、筆者は脱線が大好きである。必要に応じて適当に読み飛ばしてください。
地震計の大まかな構成
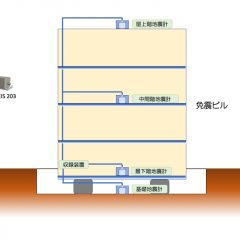
地震計の話と言ってもするのは検出器の話だが、意外と検出器と収録器が分かれていたりGPSアンテナが必要だったり管理用にパソコンが必要だったりする基本的な構成の話が知られていないので、混同を防ぐためにも本題に入る前に軽く触れておこう。下図は一般的なダムを想定した比較的小規模の地震観測システムのブロック図である。
地震観測システムブロック図例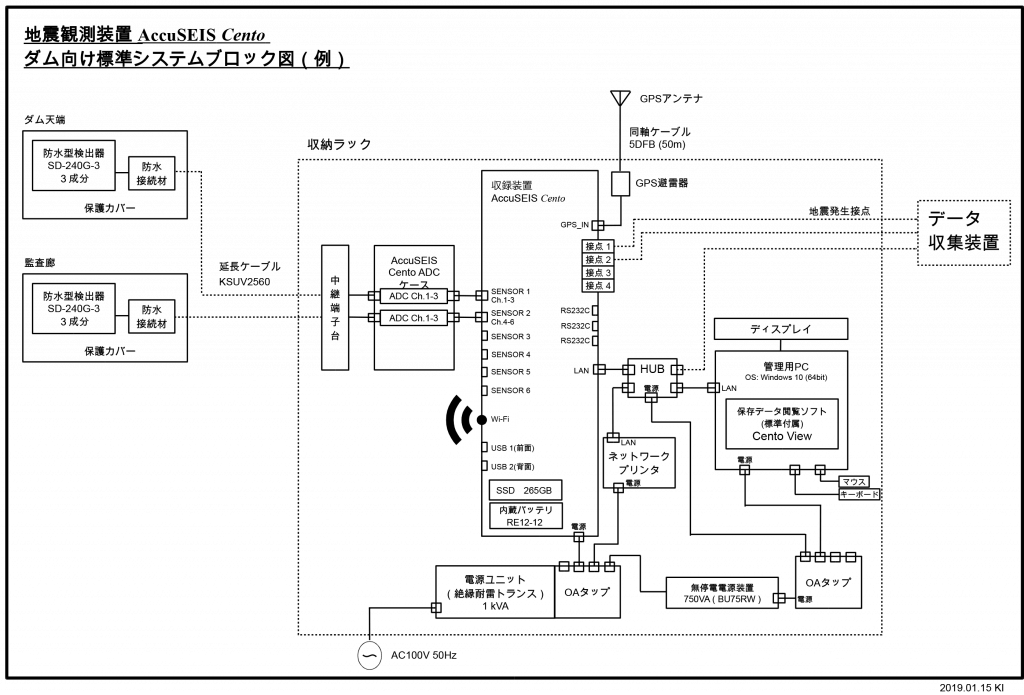
所定の位置に設置したFB型検出器2台がフィードバックアンプ、アンプ、ADCを兼ねた装置(製品としてはまとめてADCと呼んでいる)を介して収録装置に接続されている。FB型検出器は電子基板を内蔵しない機械式でADCと離して設置できるため、埋設など故障によって交換のしにくい場所の観測に向いている。収録装置はGPSアンテナで拾った時刻信号をADCに送り、アナログ信号をデジタルに変換するタイミングを管理している。ADCでデジタルに変換された信号は時刻やセンサー感度といった付随する情報と共に収録装置に保存される。また、収録装置は受信したデータを常時解析し予め与えられた条件を満たした時に、データを特別に切り取りイベントデータとして保存したり、外部の管理システムへ向けて情報を送信したりする。収録装置の設定を変更したり、保存されたデータを閲覧したり取り出すのには管理用パソコンが用いられる。一般的には故障しにくいFAPCに専用の管理ソフトをインストールして運用する。と言っても収録装置Centoは簡単な設定なら本体表示部でできるし、データの取得もUSBメモリを挿すだけでできる。PCを介した操作も一般的なウェブブラウザ(推奨はGoogle Chrome)で行うので、実は専用パソコンを用意する必要もなく、Wi-Fiオプションをつけるか無線LANルーターを接続すればタブレット端末やスマホでも管理できる。なんならデータもネットワークで接続された外付けの記憶媒体に自動で保存することもできる。
なんとなく雰囲気はわかっていただけただろうか。場所によっては検出器が10台20台と言った大規模システムもあるし、検出器と収録装置を一台ずつセットで日本中に設置しネットワーク経由で管理することもある。この記事で扱うのはこの内で検出器からADCまでの基本的な部分だ。
おまけ
頑張って読もうとしてくれる中学生高校生、数学に全く触れてこなかった大人のために、三角関数や指数関数の微分など使う公式を並べておく。詳しい話は高校数学の参考書を見てほしい。このくらいの話ならネット上でも詳しい解説が沢山見つかる。もちろんそんな事は当たり前だと言う人は読み飛ばしてください。
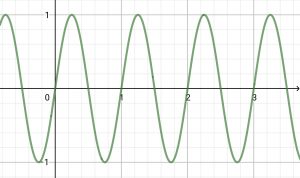
・サイン関数 y=\sin{2\pi x}
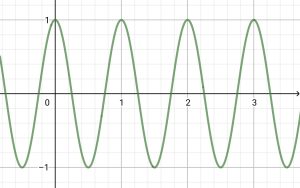
・コサイン関数 y=\cos{2\pi x}
・三角関数の関係
\begin{aligned} \tan&{x}=\frac{\sin{x}}{\cos{x}}\\ \sin&{(-x)}=-\sin{x}\\ \cos&{(-x)}=\cos{x}\\ \sin&{(a+b)}=\sin{a}\cos{b}+\cos{a}\sin{b}\\ a\sin&{x}+b\cos{x}\\ =&\sqrt{a^2+b^2}\bigl(\frac{a}{\sqrt{a^2+b^2}}\sin{x}+\frac{b}{\sqrt{a^2+b^2}}\cos{x}\bigr)\\ =&\sqrt{a^2+b^2}\bigl(\sin{x}\cos{d}+\cos{x}\sin{d}\bigr)\\ =&\sqrt{a^2+b^2}\sin{(x+d)}\\ \bigl(\cos&{d}=\frac{a}{\sqrt{a^2+b^2}},\sin{d}=\frac{b}{\sqrt{a^2+b^2}}\bigr)\\ \end{aligned}
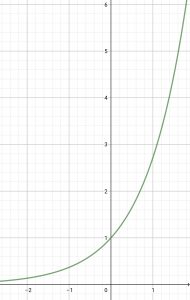
・指数関数 y=e^{2\pi x}
・微分の定義式
y(x)'=\frac{dy}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}
雑にいうと微小区間の変化量の平均値のこと。y(x)が移動距離を表すとすればある時間xからx+hまでの平均速度を表す式になっていることがわかるだろうか?hを限りなく0に近づけてあげると、つまりこれは時間xの時の速度を表している。
これをもう一度微分した
y''=\frac{d^2y}{dx^2}
は加速度になる。
・微分の公式を幾つかと、代表的な関数の微分
\begin{aligned} f'(g(x))&=g'(x)f'(g(x))\\ \bigl(f(x)g(x)\bigr)'&=f'(x)g(x)+f(x)g'(x)\\ \\ y&=ax^2+bx+c\\ y'&=2ax+b\\ y''&=2a\\ \\ (a\sin{\omega x})'&=\omega a\cos{\omega x}\\ (a\cos{\omega x})'&=-\omega a\sin{\omega x}\\ (ae^{\omega x})'&=\omega ae^{\omega x}\\ \end{aligned}
・虚数iとオイラーの公式
\begin{aligned} i&=\sqrt{-1}\\ i^2&=-1\\ e^{i\omega x}&=\cos{\omega x}+i\sin{\omega x} \end{aligned}
不十分な気もするけれど、キリもないのでこのくらいにしておこう。
最後にここまで読んでくれた勉強熱心な方のためにグラフ計算サイトDesmosを紹介しておく。基本的に平面図形しか取り扱えないが、式を書いてあげれば簡単にグラフにしてくれる素晴らしいサイトだ。スマホアプリもある。他にもGeoGebraなども有名だ。こちらは立体も扱える。もっと高度な計算をしてくれるサイトとしてはWolframAlphaなどが有名だろうか。
おまけとしてバネ運動の例を置いておく。パラメータとして質量、バネ定数、初期位置、初期速度を変えられるようになっているの遊んでみていただければ幸いである。右下のDesmosのロゴ(表示されない場合はリンク)をクリックするとこのグラフのページに飛ぶことができる。
https://www.desmos.com/calculator/4rtinokjt1
| 本項 | 次へ 地震計の物理学2-道化師のダンス- |